 Dopo aver riascoltato quest'interessantissima trasmissione radiofonica di Piergiorgio Odifreddi ho pensato di ripercorrere e approfondire (per quanto possa consentirlo un blogghetto) l'avvincente percorso storico tra Numeri e Geometria che parte da Pitagora per arrivare alla fine del XX secolo.
Dopo aver riascoltato quest'interessantissima trasmissione radiofonica di Piergiorgio Odifreddi ho pensato di ripercorrere e approfondire (per quanto possa consentirlo un blogghetto) l'avvincente percorso storico tra Numeri e Geometria che parte da Pitagora per arrivare alla fine del XX secolo. Per molto tempo l'uomo usò il concetto di numero, le strutture geometriche e le verità (teoremi) relative ad essi in modo piuttosto automatico, utilitaristico e inconsapevole: i numeri erano molto utili; nella vita quotidiana, ma soprattutto nei commerci e in molte delle sette arti.
Per molto tempo l'uomo usò il concetto di numero, le strutture geometriche e le verità (teoremi) relative ad essi in modo piuttosto automatico, utilitaristico e inconsapevole: i numeri erano molto utili; nella vita quotidiana, ma soprattutto nei commerci e in molte delle sette arti.Quando si svilupparono civiltà più ricche e potenti che potevano permettersi di mantenere dei pensatori, si cominciò a riflettere sulla natura delle suddette entità numeriche e geometriche e soprattutto sulle verità (teoremi) relative ad esse.
 Tra i primi (520 a.C circa) a sviluppare questo tipo di pensiero ci furono Pitagora e i pitagorici (una sorta di setta mistico/scientifica).
Tra i primi (520 a.C circa) a sviluppare questo tipo di pensiero ci furono Pitagora e i pitagorici (una sorta di setta mistico/scientifica).Il motto dei pitagorici era: Tutto è Numero. Dove per Numero i pitagorici intendono numero intero; e cioè l'insieme dei numeri {1,2,3,4,ecc.} che in matematica moderna viene anche denominato insieme dei numeri naturali e rappresentato con
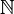
Inoltre i pitagorici conferivano al numero un significato mistico, che andava oltre quello astratto/calcolistico. Per i pitagorici il numero era anche qualcosa di reale di concreto.
In più, secondo la scuola, il mondo era costituito da Numeri e rapporti tra di essi; e cioè dall'insieme dei numeri {1,1/2,1/3,1/4,..., 2,2/3,2/5...3,3/2,3/4,ecc.} che in matematica moderna viene anche denominato insieme dei numeri razionali (da ratio, rapporto) e rappresentato con

Dunque il mondo sarebbe stato completamente misurabile (nei suoi vari fenomeni, in biologia, in astronomia, in musica, in fisica), e la comprensione dei numeri avrebbe consentito la comprensione dell'esistenza stessa. La "misurabilità" del mondo avrebbe quindi conferito alla realtà della natura ordine e armonia.
Finché un giorno qualcuno della scuola non si accorse che la diagonale del quadrato non può essere misurata in termini di lato del quadrato. Cioè se assumiamo il lato come nostra unità di misura non riusciremo mai ad esprimere un rapporto di numeri interi che possa rappresentare la lunghezza della diagonale.
Questa scoperta creò dei problemi. Di che tipo? Lo vedremo nella prossima puntata....
Indice della serie
8 commenti:
grazie del link, me lo ascolteró
CIao Arimortis !
Non c'è di che!
Buona serata
e' proprio che i numeri non mi amano.
gia' la prima lezione mi ha creato qualche problema nell'ultima parte, figuriamoci con la seconda come sara'.
il teorema di pitagora e' il mistero di pitagora. per intenderci.
i pitagorici me li ricordo dalla filosofia del liceo. that's all I can do.
valeriascrive
volevo dire puntata, non lezione.
sbaglio proprio l'approccio.
;)
Ciao Crazy time!
Mi fa già molto piacere che tu l'abbia letto fino alla fine! Grazie!
La maggior parte della gente di solito si annoia molto sentendo queste cose. Invece per me sono come il nettare per un ape :-)
Soprattutto in questo periodo poi che sto avendo un rigurgito di mio passato matematico.
Ascoltando queste trasmissioni radiofoniche matematico/divulgative mi convinco sempre di più che la matematica viene spesso insegnata male. Come qualcosa di polveroso e fossilizzato. E invece è tutt'altro. Forse si insegna troppo formalismo e poco contesto storico/semantico.
Molto belle sono anche queste puntate di Franco Ghione a Damasco.
Che cosa ti ha creato problemi nell'ultima parte? Il fatto la diagonale del quadrato non può essere misurata in termini di lato del quadrato?
Detto in altri termini è come dire che se tu hai un quadrato, prendi il lato come tuo metro e cerchi di misurarci la diagonale, ti accorgerai che il tuo metro non basta, perché la diagonale è più lunga. Dovrai quindi aggiungere al tuo metro un pezzetto, ad esempio 1/4 (0,25) di metro. Così avrai 1,25. Non basta ancora. Aggiungi la metà di un quarto, ma non basta ancora..... e così via. Cioè non riuscirai mai a trovare un frazione del tuo metro che aggiunta ti possa misurare la diagonale. O andrai troppo oltre o rimarrai troppo indietro.
Ho complicato ancora di più le cose forse...
Ho letto del professore sul tuo blog. Mi ricorda la nostra insegnante di tedesco in quanto a energia...
Saluti
Crazy time,
volevo completare la risposta con un commento alla tua citazione
il teorema di Pitagora come il mistero di Pitagora.
In realtà in un qualche modo è vero. Per ironia della sorte infatti i pitagorici trovarono la loro bestia nera celata proprio nel famoso teorema del Maestro.
Dovettero essere infatti molto sorpresi che un caso particolare del teorema conduceva proprio all'incommensurabile che faceva crollare la loro mistica/teoria.
Infatti se consideriamo triangolo rettangolo di lato 1 e chiamiamo x la lunghezza incognita dell'ipotenusa, il teorema ci dice che 1² + 1² = x².
Da cui, sommando 1² + 1² = 2 = x².
Estraendo quindi la radice da ambo le parti:
radice di 2 = x
La lunghezza dell'ipotenusa (che coincide poi con la diagonale del quadrato di lato 1) coincide quindi con la bestia nera incommensurabile.
non hai complicato le cose ;)
so che la matematica la insegnano male a scuola. come un po' tutto il resto.
Grazie per la rassicurazione :-)
Buona domenica!
Posta un commento