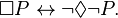Chi vincerà il mondiale del 2014? Una questione di Logica intuizionista? - Appendice 2

Nell'appendice numero uno dicevamo che tra le principali differenze della Logica intuizionista rispetto alla Logica classica c'è sia la non validità del principio del terzo escluso che la non validità dell'equivalenza tra affermazione e doppia negazione (I ↔ ¬¬I).

Usando quindi gli strumenti della Logica intuizionista, non sì potrà ad esempio dedurre la profezia Italia '14 (P="o l'Italia vincerà il mondiale del 2014 oppure l'Italia non vincerà il mondiale del 2014").
Inoltre, usando l'intuito, molti di voi probabilmente direbbero che affermare che l'Italia vincerà il mondiale del 2014 è equivalente a dire che non è vero che l'Italia non vincerà il mondiale del 2014.
O detto in termini simbolici:

I ↔ ¬¬I

Invece nella Logica intuizionista, dal fatto che l'Italia vincerà il mondiale del 2014 si potrà sì dedurre che non è vero che l'Italia non vincerà il mondiale del 2014 ( I → ¬¬I ), ma non vale il viceversa. Cioè dal fatto che non è vero che l'Italia non vincerà il mondiale del 2014 non si potrà dedurre che l'Italia vincerà il mondiale del 2014 (¬¬I → I).

A questo punto risulta sicuramente interessante vedere molto brevemente qualche cenno di semantica per la Logica intuizionista. È infatti grazie ad essa che possono essere verificate le suddette affermazioni.
Il primo a fornire una semantica per la Logica intuizionista fu Heyting, un allievo di Brouwer.
In modo simile alla semantica per la Logica proposizionale classica, in cui l'algebra booleana viene usata per stabilire se una formula sia vera o falsa, Heyting pensò di introdurre un nuovo tipo di algebra, chiamata in seguito algebra di Heyting, per stabilire se una formula sia vera o falsa nell'ambito della Logica intuizionista.

La Logica proposizionale classica, come la maggior parte dei sistemi di Logica matematica, è costituita da una parte sintattica ed una parte semantica.La parte sintattica è quella che si occupa di definire la corretta struttura delle formule; e nella quale si include di solito anche l'apparato deduttivo che definisce gli assiomi e le regole che consentono di dedurre i teoremi a partire dagli assiomi.
Mentre la parte semantica, che risulta di solito più semplice ed intuitiva, è quella che si occupa di definire il significato dei simboli.

Per definire una semantica della Logica proposizionale classica si può partire ad esempio da una funzione di valutazione che va dall'insieme L delle formule all'insieme {V,F} (vero, falso). O detto in termini più semplici, si definisce un meccanismo per determinare in quali casi una formula sia vera o falsa. La funzione la si definisce nel seguente modo:

v : L → {V,F}

tale che per ogni coppia di formule A e B valgano le seguenti condizioni (sse sta per se e solo se):

v(¬A) = V sse v(A) = F  (¬A è vera sse A è falsa)

v(¬A) = F sse v(A) = V  (¬A è falsa sse A è vera)

v(A∧B) = V sse v(A) = V e v(B) = V  (A∧B è vera sse A è vera e B è vera)

v(A∨B) = V sse v(A) = V oppure v(B) = V  (A∨B è vera sse A è vera oppure B è vera)

v(A→B) = V sse v(A) = F oppure v(B) = V  (A→B è vera sse A è falsa oppure B è vera)

Ciò che collega la sintassi con la semantica sono i teoremi di completezza, il cui scopo è dimostrare l'equivalenza tra il concetto di dimostrabilità sintattica ed il concetto di verità semantica. Nel caso particolare della Logica classica (sia proposizionale che predicativa) interviene il Teorema di completezza di Gödel (da non confondere con il Teoremi di incompletezza di Gödel) ad asserire che una formula è dimostrabile sse è vera per ogni funzione di valutazione.

Similmente, anche nel caso della Logica proposizionale intuzionista si può definire una funzione di valutazione, ma di tipo un po' diverso. Invece di essere correlata ad un'algebra booleana la funzione di valutazione della Logica proposizionale intuzionista è correlata ad un'algebra di Heyting.
Ad esempio si può definire la funzione di valutazione che va dall'insieme L delle formule all'insieme dei sottinsiemi aperti della retta reale:

v : L → {int(S) : S ⊆ R} dove int(S) è la parte interna di S

tale che per ogni coppia di formule A e B valgano le seguenti condizioni:

v(A) = int(v(A))

v(¬A) = int(v(A)^C) dove X^C è il complemento di X

v(A∧B) = v(A) ∩ v(B)

v(A∨B) = v(A) ∪ v(B)

v(A→B) = int(v(A)^C ∪ v(B))

Anche in questo caso intervengono teoremi di completezza a dirci che le formule dimostrabili della Logica intuzionista coincidono con quelle valide e che queste ultime sono esattamente quelle per cui v(A) = R per ogni scelta di v. Cioè quelle a cui la funzione di valutazione associa l'insieme più grande: tutta la retta reale.

Grazie a questi teoremi si può facilmente verificare che la formula ¬(A ∧ ¬A) è valida. Il fatto che questa formula risulti valida è un requisito minimale affinché un sistema di Logica matematica possa destare qualche interesse. Se essa risultasse non valida infatti esisterebbero delle A per cui il sistema potrebbe dimostrare sia A che ¬A. Il sistema risulterebbe quindi contraddittorio.
La validità di ¬(A ∧ ¬A) si può dimostrare in quanto ponendo v(A) = X, indipendentemente dall'insieme X che viene scelto come valore della formula A, il valore di ¬(A ∧ ¬A) sarà sempre uguale all'intera retta reale R. Infatti

v(¬(A ∧ ¬A)) =

int((v(A ∧ ¬A))^C) =

int((v(A) ∩ v(¬A))^C) =

int((X ∩ int((v(A))^C))^C) =

int((X ∩ int(X^C))^C) =

(Siccome int(X^C) è un sottinsieme di X^C allora

X ∩ int(X^C) = ∅)

int((∅)^C)=int(R)=R

Invece si può facilmente mostrare che il principio del terzo escluso (A ∨ ¬A) non è valido. A tal scopo è sufficiente trovare una particolare funzione di valutazione v per cui risulti v(A ∨ ¬A) ≠ R.
Basta scegliere v(A) = {x ∈ R : x > 0 }. Si avrà infatti:

v((A ∨ ¬A)) =

v(A) ∪ v(¬A) =

v(A) ∪ int(v(A)^C) =

{x ∈ R : x > 0 } ∪ int({x ∈ R : x ≤ 0 }) =

{x ∈ R : x > 0 } ∪ {x ∈ R : x < 0 }) =

{x ∈ R : x ≠ 0 } ≠ R che è ciò che si voleva dimostrare

Potremo quindi finalmente concludere che usando gli strumenti della Logica intuizionista, non sì può dedurre la profezia Italia '14.

Ho anche provato a dimostrare che nella Logica intuizionista vale (I → ¬¬I), ma non vale il viceversa (¬¬I → I). Per chi fosse interessato può dare uno sguardo a questo mio tentativo di dimostrazione.

Merluzzo essiccato in veranda: Bodø - Stamsund - Svolvær (Norvegia 17)

7 giugno 2009

Alle 15 ci siamo reimbarcati sulla Midnatsol alla volta delle Lofoten.


View Larger Map

La traversata tra terra ferma e arcipelago dura più di quattro ore.

Il primo approdo alle Lofoten è al porto di Stamsund.

Sbarchiamo giusto per curiosare un po' qua e la.
Trovo deliziosa questa immagine di merluzzo a cui l'essiccazione in questa lignea veranda conferisce una qualità di divenendo stoccafisso.
Dopo mezzora ci reimbarchiamo.

I ponti che collegano le isolette dell'arcipelago sono degni di nota. Alcuni sono dotati di inconsuete curvature e torsioni.

Dopo un'altra ora di navigazione, verso le 21, sbarchiamo a Svolvær.

Altre foto: Bodø - Stamsund, Stamsund, Stamsund - Svolvær

Giornate precedenti ....

Chi vincerà il mondiale del 2014? Una questione di Logica intuizionista? - Appendice 1

Paolo Rossi e Socrates: storica partita
Italia - Brasile 3 -2 (1982)

Nella precedente discussione dicevamo che prendendo una squadra a caso tra quelle che hanno fatto una pessima figura nella fase finale del mondiale di calcio 2010, come l'Italia ad esempio, potremmo formulare la seguente
profezia Italia '14 (che chiameremo P):


P = "o l'Italia vincerà il mondiale del 2014 oppure l'Italia non vincerà il mondiale del 2014"

O detto in termini simbolici, indicando con I la proposizione Italia '14 ("l'Italia vincerà il mondiale del 2014") potremmo scrivere:

P = (I oppure non-I)

che si può anche scrivere come:

P = (I ∨ ¬I)

Quella che abbiamo appena scritto la si può anche vedere come la formula che descrive in termini simbolici il Principio del terzo escluso. La profezia Italia '14 è quindi un esempio di Principio del terzo escluso. Terzo escluso in quanto la ragione ci porterebbe a dire che non esiste una terza alternativa nell'affermazione "o l'Italia vincerà il mondiale del 2014 oppure l'Italia non vincerà il mondiale del 2014".
Ma è proprio così? Sì può asserire che P = (I ∨ ¬I) è sempre vera? Che non esiste una terza alternativa?

Penso che, a differenza della profezia Maya, nessuno dei membri della comunità scientifica, tranne forse qualche vetero-intuizionista, proverebbe a contraddire la profezia Italia '14...
Certo però che se la profezia Maya dovesse rivelarsi nel frattempo valida....
Bè, in tal caso potremmo forse dire che è vera ¬I, anche se in quel caso nessuno sarà in grado di attestare che l'Italia non ha vinto il mondiale del 2014.
Eppure ci sono stati dei logico-matematici che hanno posto dubbi sulla validità del principio del terzo escluso. L'approccio sostenuto da tali logico-matematici fu definito intuizionismo.
Vediamo quindi con un po' più di precisione che cos'è questo intuizionismo.

Ho già citato il fatto che il mio dialogo immaginario della precedente puntata tra Brouwer e Hilbert è ispirato ad una reale controversia tra i due matematici che va inquadrata tra le appassionanti discussioni di fine '800 primi del '900 relative ai fondamenti della matematica  e che tra le posizioni filosofiche ipegnate nella rifondazione dei fondamenti c'era quella costruttivista con Poincaré e Weyl, all'interno della quale si posizionava la corrente radicale degli intuizionisti con Brouwer.
I costruttivisti, contrapponendosi principalmente al pensiero di Hilbert e dei formalisti, affermavano la necessità di trovare o di costruire un oggetto matematico per poterne dimostrare l'esistenza rifiutando le dimostrazioni per assurdo soprattutto nei casi che coinvolgono l'infinito; inoltre la corrente intuizionista dei costruttivisti, capeggiata da Brouwer (mi sembra quasi di stare a descrivere un partito), si spingeva oltre il costruttivismo rifiutando più in generale le dimostrazioni che implicano l'utilizzo di insiemi infiniti e l'applicazione in questi casi dei ragionamenti basati sul principio del terzo escluso.

Oggi si può probabilmente affermare che l'intuizionismo, come prospettiva filosofica volta a rifondare la matematica, ebbe un successo piuttosto limitato; anche se generò utili e prolifiche discussioni. Tuttavia lo stesso non si può dire per il sistema formale della Logica Intuizionista sviluppato da Arend Heyting, un allievo di Brouwer. Tale sistema formale ha dato luogo infatti ad una serie di sviluppi della Logica e ha trovato inoltre diverse applicazioni nell'informatica, sia teorica che applicata.

Tra le principali differenze della Logica intuizionista rispetto alla Logica classica c'è sia la non validità del principio del terzo escluso che la non validità dell'equivalenza tra affermazione e doppia negazione (I ↔ ¬¬I).
Ovvero, tralasciando per un attimo il rigore matimatico, si può dire che usando gli strumenti della Logica intuizionista, non sì potrà ad esempio dedurre la profezia Italia '14.
Inoltre, usando l'intuito, molti di voi probabilmente direbbero che affermare che l'Italia vincerà il mondiale del 2014 è equivalente a dire che non è vero che l'Italia non vincerà il mondiale del 2014.
O detto in termini simbolici:

I ↔ ¬¬I

Invece nella Logica intuizionista, dal fatto che l'Italia vincerà il mondiale del 2014 si potrà sì dedurre che non è vero che l'Italia non vincerà il mondiale del 2014 ( I → ¬¬I ), ma non vale il viceversa. Cioè dal fatto che non è vero che l'Italia non vincerà il mondiale del 2014 non si potrà dedurre che l'Italia vincerà il mondiale del 2014 ¬(¬¬I → I).

A questo punto risulterebbe sicuramente interessante dare un breve sguardo alla semantica per la Logica intuizionista. È infatti grazie ad essa che possono essere verificate le suddette affermazioni. Ma questo lo vedremo nell'appendice numero due.

50mila

Nina Zilli



Cinquantamila lacrime non basteranno perchè
musica triste sei tu dentro di me.
Cinquantamila pagine gettate al vento perchè
eterno è il ricordo, il mio volto per te.
Non ritornare, no tu non ti voltare, non vorrei mi vedessi cadere.

A me piace così, che se sbaglio è lo stesso, perchè questo dolore è amore per te.
Cinquantamila lacrime senza sapere perchè
sono un ricordo lontano da te.

Cinquantamila lacrime non basteranno perchè
musica triste sei tu dentro di me.
Non mi guardare, non lo senti il dolore, brucia come un taglio nel sale.

A me piace così, che se sbaglio è lo stesso, perchè questo dolore è amore per te.
A me piace così, e non chiedo il permesso, perchè questo dolore è amore per te.

Milca

La nostra amata Milca ha subito un infortunio un po' bruttino. Speriamo si riprenda.

Mine vaganti ("Männer al dente"!?) - Ferzan Ozpetek

Siamo appena tornati dalla visione di Mine vaganti di Ozpetek. In generale, quando riusciamo a capire la lingua originale, noi evitiamo le versioni doppiate ma stavolta non avevamo scelta e ci siamo dovuti accontentare della versione doppiata in tedesco. La prima cosa strana era il titolo tradotto opinabilmente come "Männer al dente" ("Uomini al dente"). Un'altra cosa che mi ha disturbato era il finto accento italiano che ogni tanto veniva inserito qua e là dai doppiatori tedeschi.

Nonostante il doppiaggio la pellicola è piaciuta molto sia a me che a Zucchero. A giudicare dalle reazioni del pubblico deve essere piaciuta molto anche al resto della sala. La signora che sedeva alla mia destra ha riso a crepapelle per la maggior parte delle scene comiche, mentre alla fine ha consumato diversi fazzolettini per asciugarsi le lacrime. Ho l'impressione che il film avrà successo in Germania.

Qualche scena

Cinquantamila lacrime - Nina Zilli

Sopravviveremo alla discesa nel Maelstrom di Edgar Allan Poe? (Norvegia 16: Bodø)

7 giugno 2009

Alle 12:30 sbarchiamo a Bodø. Abbiamo prenotato il "Safari marino" che ci dovrebbe condurre nel mezzo della Saltstraumen, la corrente mareale generatrice di gorghi più potente del mondo, più forte addirittura della celebre Maelstrøm di poeiana memoria: l'immenso gorgo che trascina all'interno ogni cosa. Una sorta di buco nero marino! (E chi non conosce Una discesa nel Maelström di Edgar Allan Poe!?).
Riusciranno i nostri prodi a sopravvivere alle insidie dei terrificanti gorghi che generose travolsero alme d'eroi?

Sprezzanti del pericolo,

indossano gli scafandri,

e si avviano.

La prima tappa è prevista presso un affioramento di resti dell'orogenesi caledoniana (Caledonian fold belt). Le forme, le superfici e le stratificazioni, plasmate in queste rocce dalle collisioni paleocontinentali di circa 450 milioni di anni fa, sono strabilianti.

Ci gettiamo infine in pasto agli spietati gorghi. Dopo titaniche battaglie contro i marosi riusciamo a riemergere indenni. Il colossale scontro segna tuttavia irreversibilmente i nostri volti che mostrano ai reciproci sguardi gli impietosi segni di un invecchiamento decennale: Edgardo aveva proprio ragione!

La nostra audacia verrà infine premiata dall'avvistamento fotograficamente immortalato di una semi-invisibile aquila di mare.

Alle 15 ci reimbarchiamo sulla Midnatsol alla volta delle Lofoten.

Altre foto ....

Giornate precedenti ....

James Senese: statte zitt' tu si niro - si chiammava Carlucciello...

JamesSenese: bel personaggio, belle interviste.

James Senese: "si chiammava Carlucciello..."

Carnevale della Matematica #27

Oggi è il14 luglio e oltre a commemorare la presa della Bastiglia segnaliamo anche la nuova puntata del Carnevale della Matematica, la n. 27, ospitata dal fondatore del Carnevale della Matematica Maurizio Codogno su il Post, il giornale on-line di Luca Sofri.

Il numero degli articoli stavolta è un po' più ridotto, forse a causa del clima e delle vacanze, ma la qualità continua ad essere ottima.
Il mio contributo viene introdotto in questo modo:

Dionisoo nel suo Blogghetto scomoda nientemeno che Brouwer e Hilbert per fare una previsione sul risultato dell’Italia nei prossimi mondiali di calcio del 2014 (profezia dei Maya permettendo), portando il lettore a capire se e come si possono usare le dimostrazioni per assurdo e con insiemi infiniti.

Il 14 agosto, l'edizione ferragostano-vacanzierissima - la numero 28 - del Carnevale della Matematica sarà ospitata da Zar sul blog Gli studenti di oggi.

Calendario con le date delle prossime edizioni del Carnevale

Pagina fan del Carnevale su Facebook

Il ciclo delle notizie scientifiche

Immagine copiata dal post Il ciclo delle notizie scientifiche su D I S . A M B . I G . U A N D O

Norvegia 15: Rørvik - Bodø: ingresso nel Circolo Polare Artico

7 giugno 2009

La sera prima siamo andati a letto verso l'una visto che il giorno successivo si presenta privo di impegni mattutini e quindi adatto per una lunga dormita.


View Larger Map

Mentre sogno notti polari illuminate da variopinte aurore boreali una voce sgraziata mi perfora i timpani. Do uno sguardo all'orologio. Sono le 7. La voce proveniente dall'altoparlante della nostra cabina continua a gracchiare il suo annuncio. Stavolta in lingua inglese: tra dieci minuti attraverseremo il circolo polare artico.
Zucchero dice: vabbè, oramai siamo svegli, andiamo a fotografare l'isoletta con il mappamondo.

Mentre la guardo tra un misto di intorpidimento onirico-interruptus e riluttanza, Zucchero si è già vestita. Cerco di inseguirla. Ma né io né Zucchero riusciamo ad arrivare in tempo sul ponte. Ci dobbiamo quindi accontentare di una visione filtrata dal vetro sporco del mappamondo che demarca il circolo polare.

Altre foto scattate nel tratto di mare tra Rørvik e Bodø.

Ulteriori foto scattate nel tratto di mare tra Rørvik e Bodø....

Giornate precedenti ....

Grigorij Perelman rifiuta 1 milione di dollari!? La risposta è sì!

Ne avevo parlato qui.
La decisione è stata finalmente presa qualche giorno fa. Grigorij Perelman ha rifiutato 1 milione di dollari!

Pare che la motivazione principale sia stata il disaccordo con la comunità dei matematici: "I don’t like their decisions; I consider them unjust".

Chi vincerà il mondiale? Una questione di Logica intuizionista?

Scegliamo una squadra a caso tra quelle che hanno fatto una pessima figura nella fase finale del mondiale di calcio 2010. L'Italia ad esempio.
Potremmo già formulare un pronostico sui risultati dell'Italia ai modiali brasiliani del 2014?
Bè, potrei affermare ad esempio che:

o l'Italia vincerà il mondiale del 2014 oppure l'Italia non vincerà il mondiale del 2014

Penso che pochi proverebbero a contraddirmi. Ma siamo proprio sicuri che non ci sia un'altra possibilità? O come direbbe qualcuno, siamo proprio sicuri che tertium non datur?

Qualche notte fa dopo una cena a base di insalata di farro annaffiata da un paio di bicchieri di Regaleali me ne sono andato a letto con un certa sensazione di completezza e soddisfazione. In piena notte vengo però svegliato dall'impressione di un lamento profondo. In piedi accanto al mio letto scorgo una tenebrosa figura antropomorfa. Mi pietrifico all'istante. Dalla figura proviene una voce: quasi un infrasuono.
B: (rabbioso tormentato) Perché non vuole ammetterlo!! L'intuzione e la costruzione sono alla base di tutto!
Eppure in gioventù lo ammiravo così tanto.... E anche lui mi stimava molto.
D: (ripresosi dal trauma riesce timidamente a profferire parola) Scusi, ma lei chi è?
B: (austero e marziale) Molto lieto! Luitzen Egbertus Jan Brouwer. Ma lei può chiamarmi semplicemente professor Brouwer.
D: (reverenziale un po' più animato) E di chi sta parlando professor Brouwer?
B: (spazientito) Come di chi!? Ma del professor David Hilbert naturalmente.

Una seconda figura si materializza nella stanza.

H: (con voce tuonante) Ho sentito pronunziare il mio nome!
B: (con enfasi accigliata) Stavo per l'appunto cercando di dire che la nostra aspirazione deve essere la ricerca della verità, non un arido formalismo alieno da essa.
H: (con sufficienza?) Ma con il mio formalismo saremo in grado di svelare e rivelare la verità in modo automatico e univoco. Potremmo anche giungere ad un punto in cui le presenza umana sarà superflua nel processo di disvelamento delle verità ignote.
B: (categorico) Ma voi, caro Hilbert, partite da premesse sbagliate! Per dimostrare l'esistenza di un oggetto io dovrò mostrare quell'oggetto o almeno mostrare di saperlo costruire.
H: (contraddittoriamente) No! Non è affatto vero! La costruzione appesantisce e complica inutilmente le cose. Brevità ed economia di pensiero! Sono queste le ragioni d'essere delle dimostrazioni d'esistenza. L'oggetto o esiste o non esiste. Tertium non datur! E se assumendo la sua non esistenza giungo ad una contraddizione allora vorrà dire che l'oggetto dovrà necessariamente esistere!
B: (quasi con soddisfazione) Ed ecco che abbiamo introdotto anche le più fallaci tra le vostre assunzioni: le dimostrazioni per assurdo e peggio ancora il principio del Terzo escluso. L'accettazione acritica di tali strumenti solo perché riconducibili a Pitagora e Aristotele è inammissibile!
H: (con scoraggiato scherno) Ma proibire ad un matematico l'uso del principio del terzo escluso sarebbe come proibire a un pugile di usare i pugni o proibire ad un astronomo di usare il telescopio. 
B: (in un crescendo di impeto) La matematica non è un giochino enigmistico privo di significato! I suoi oggetti non sono scorrelati dalla realtà!! Le sue regole formali non possono prescindere dall'intuito!!! La scelta dei suoi assiomi deve essere guidata dall'esperienza!!!!

Le figure svaniscono dissolvendosi lentamente.

Ma allora è vero che o l'Italia vincerà il mondiale del 2014 oppure l'Italia non vincerà il mondiale del 2014? O detto in termini simbolici, indicando con I la proposizione "l'Italia vincerà il mondiale del 2014", è vero che (I ∨ ¬I)?

Forse per il caso di questo enunciato la risposta è sì. (A patto che la profezia Maya non non si riveli nel frattempo valida, ma in tal caso potremmo dire che è vera ¬I, anche se probabilmente nessuno sarà in grado di verificarlo.) Nella matematica tuttavia esistono degli enunciati che non possono essere né provati né refutati, e cioè, approssimando un po', non può essere stabilito né che siano veri né che siano falsi, e sono per questo detti indecidibili. Esempi ne sono l'assioma della scelta e l'ipotesi del continuo, che sono entrambi indecidibili nell'assiomatizzazione tradizionale della teoria degli insiemi.

Il mio dialogo immaginario tra Brouwer e Hilbert è ispirato ad una reale controversia tra i due matematici che va inquadrata tra le appassionanti discussioni relative ai fondamenti della matematica avvenute tra la fine dell'800 e i primi decenni del '900. In questo contesto le posizioni filosofiche che si contendevano il primato erano essenzialmente tre: quella logicista con Frege e Russell; quella formalista con Hilbert; e infine quella costruttivista con Poincaré e Weyl, all'interno della quale si posizionava la corrente radicale degli intuizionisti con Brouwer. I logicisti volevano rifondare la matematica a partire dalla Logica, i formalisti volevan formalizzare la matemitica entro un sistema assimoatico capace di dimostrare o refutare un qualsiasi enunciato, mentre i costruttivisti affermavano la necessità di trovare o di costruire un oggetto matematico per poterne dimostrare l'esistenza rifiutando le dimostrazioni per assurdo soprattutto nei casi che coinvolgono l'infinito; infine l'intuizionismo di Brouwer si spingeva oltre il costruttivismo rifiutando più in generale le dimostrazioni che implicano l'utilizzo di insiemi infiniti e l'applicazione in questi casi dei ragionamenti basati sul principio del terzo escluso.

In seguito un allievo di Brouwer, Arend Heyting, sviluppò l'intuizionismo come un vero e proprio sistema formale: la Logica Intuizionista. Ma questo lo vedremo nell'appendice.

Banche mondiali

Oggi la bancaria ha superato se stessa.
Ambiente: banca tappezzata di bandiere e ghirlande con i colori della bandiera.
Bancaria: gonna e maglietta con i colori della bandiera, ghirlanda al collo con i colori della bandiera, unghie dipinte con i colori della bandiera, zigomi dipinti con i colori della bandiera.
Le mancavano solo queste:



Ué ma dove siamo? In banca, in discoteca o allo stadio?

Norvegia 14: Rørvik

6 giugno 2009

Verso le 21, dopo 9 ore circa di navigazione verso nord sbarchiamo a Rørvik.
Mentre girovaghiamo per la cittadina abbigliati più o meno in questo modo veniamo superati da un paio di adolescenti in bicicletta con maniche corte e calzoncini.

Attraggono la mia attenzione questa chiesa in legno,







e questa Pizzabar-Kebab Napoli.







Il resto della serata lo passiamo sul ponte della Midnatsol.






Tiriamo fino a tardi anche perché vogliamo goderci quello che sarà l'ultimo tramonto per i prossimi sei giorni. Questo è il sole delle 23:30. Siamo a poche decine di Km dal circolo polare.

Alla fine andiamo a letto verso l'una visto che il giorno successivo si presenta privo di impegni mattutini e quindi adatto per una lunga dormita.

Altre foto: Rørvik

Giornate precedenti ....

Porto sfiga come Mick Jagger?

Ora sarei spinto a fare il tifo per Olanda e Spagna. Ma un'osservazione induttiva dei risultati precedenti mi ha portato a chiedermi: porto sfiga come Mick Jagger?
Forse dovrei astenermi? O fare il tifo per gli altri?

L'estetica del sandalo: col calzino o senza? (domande estivo-esistenziali)

È internazionalmente noto quale sia il popolo aduso a tale vezzo estetico. Ma è effettivamente così? O la diceria si va lentamente trasformando in stereotipo?

Viste le temperature sopra i trenta (36° previsti per domani) faccio sfoggio da qualche giorno dei miei infradito (finalmente a 40 anni ho imparato a camminarci decentemente).
Durante la prova di lunedì, nelle abbondanti pause presenti nella partitura trombonistica mi sono dilettato nell'interessante passatempo dell'osservazione dell'abbigliamento calzaturistico dei giovani colleghi orchestrali. E sono induttivamente giunto alle seguenti conclusioni:

1. Le giovani orchestrali indossano i sandali senza calzino (ma pare che il sandalo col calzino sia stato da sempre una prerogativa maschile)

2. I giovani orchestrali indossano puzzolenti scarpe da ginnastica (col calzino-fantasmino)

L'osservazione è stata confermata da sporadiche valutazioni extra-orchestrali.

A questo punto quali delle seguenti conclusioni potremmo dedurre?

1. I giovani non indossano più i sandali col calzino

2. Sono solo gli uomini a indossare i sandali col calzino, mentre le donne li indossano senza

3. I giovani indossano puzzolenti scarpe da ginnastica, mentre le giovani indossano i sandali senza calzino

 4. Se i sandali vengono indossati da un uomo, allora l'uomo ha più di 35 anni

Chiudo con una domanda: la tendenza è confermata anche in Italia?

Tetralogia logica

La mia tetralogia logica è stata pubblicata su Matem@ticaMente.
L'articolo viene generosamente recensito in questo modo.

Cari lettori,

pubblico un secondo contributo, tratto dal Carnevale della Matematica n.26, tra i pezzi che mi hanno colpito particolarmente. Si tratta di una interessantissima tetralogia sulla logica dal titolo "Il mondo finirà nel 2012? Una questione di Logica modale temporale?".

L'originale contributo quadripartito si giova di una serie di dialoghi immaginari, che si svolgono tra personaggi storici di eccellenza. Nella prima parte i protagonisti sono Aristotele e Diodoro Crono.

Nella seconda parte sono presentate alcune quartine, le "Rubʿayyāt" di ʿOmar Ḫayyām, in cui sono descritti i sogni e i deliri del matematico persiano Avicenna intento a dialogare con Aristotele.

Nella terza parte, mediante il duetto dialogico tra Leibiniz e Voltaire, viene considerata la "previsione" dei Maya sulla fine del mondo secondo le convinzioni della logica occidentale che, tra il 1600 e il 1700, era ai suoi albori.

Nella quarta e ultima parte, la succitata "previsione" è esaminata, tenendo conto del rivoluzionario pensiero di  Frege e Russell.

Ma mi  fermo qui, invitandovi a leggere l'accattivante tetralogia partorita dall'immaginazione di Dioniso. L'ho assemblata in un unico documento, scaricabile in versione pdf e consultabile in modalità fullscreen nel widget di Issuu (cliccare al centro del widget).

Nuova stagione musicale Auftakt Orchester: Concerto estivo

Quest'anno il Probenwochenende (fine settimana di prove) è capitato durante il nostro soggiorno italico. Ho dovuto quindi saltarlo.
Questa assenza unita al fatto che il direttore ci ha fatto saltare diverse prove. (quel "ci" si riferisce a noi tromboni (e qui mi par di sentire già la vostra battuta che mi accompagna da quando avevo 12 anni: e chi non conosce quel trombone...)). Dicevo quindi che assenza e scarsità di prove per noi tromboni, scarsità dovuta al fatto che nel programma di questa stagione suoniamo poco ma purtroppo quel poco è a tratti molto impegnativo, ci ha portato ad essere piuttosto impreparati a una paio di settimane dal concerto (che fortunatamente è stato rimandato).

Ad ogni modo questo sarà il calendario dei concerti:

mercoledì 7 luglio prova generale,
venerdì 9 alle 19:00 (prova alle 17:00) concerto all'aperto a Emmertsgrund,

domenica 11 alle 17:00 concerto all'aperto a Neckarelz,

e infine venerdì 16 alle 20:00 sarà la volta del concerto più importante a Heidelberg

Ecco il programma (che potrete pure leggere ingrandendo la locandina che vedete all'inizio del post):

1. Alexander Grigorevich Arutiunian (Arm. Ալեքսանդր Գրիգորի Հարությունյան), (alias Arutunian, Arutyunyan, Arutjunjan, Harutiunian) (23 Settembre 1920, Yerevan, Armenia): Concerto in la bemolle maggiore per tromba e orchestra(1950)



2. Johann Svendsen (Oslo, 30 settembre 1840 – Copenhagen, 14 giugno 1911) - Sinfonia N.2 in si bemolle maggiore.
Primo movimento: Allegro
Secondo movimento: Andante
Terzo movimento: Intermezzo Allegro Giusto
Quarto movimento: Finale - Allegro con Fuoco

3. Ludwig van Beethoven (1770 – 1827) - Egmont

Se vi troverete a passare da queste parti siete invitati.

E ora Forza Ghana!!

Festa danzante

La festicciola di sabato scorso per me si è aperta con la preparazione di uno dei miei cavalli di battaglia gastronomici: l'Insalata di farro con tonno, olive e capperi.
Come capita di solito ha avuto un grande successo.

Le due grosse insalatiere sono scomparse velocemente e ho ricevuto diversi complimenti e richieste di ricetta. Penso di aver trovato una combinazione di ingredienti che oltre ad essere gustosa accontenti anche i palati meno proni alla sperimentazione.

Mentre disponiamo le varie cibarie i Dissonanti montano e provano, ma quando stanno per partire con la musica i neri nuvoloni che sorvolano i cieli ciociari decidono di omaggiarci con un'acquazzone.

Dopo qualche decina di minuti la pioggia cessa e a quel punto i musicisti vogliono giustamente rifocillarsi.





Ma nonostante tutto alla fine riusciamo a ballare. E la musica va avanti per qualche ora.
Stavolta Oriana mi ha insegnato anche qualche passo di tammurriata (video d'esempio) e di danza delle spade (video d'esempio).

La truffa morale della maturità

Mi trovo piuttosto d'accordo con Massimo Gramellini. Sarebbe bello se questa fosse l’essenza della maggior parte degli italiani: integerrimi ma con delle ragionevoli eccezioni.

...Alla figlia, prima di morire, il vecchio ha spiegato che negli esami l’emotività gioca brutti scherzi, mentre con il suo metodo venivano riconosciuti i meriti e i demeriti accumulati durante l’anno. In sostanza quell’insegnante integerrimo metteva in piedi ogni estate una truffa con l’intima convinzione di rispettare una regola superiore di moralità. Non riesco a trovare una rappresentazione più efficace dell’essenza italiana. Una parte di me condanna quel professore. Ma dev’essere una parte norvegese o austro-ungarica, non fateci caso.

Tutto l'articolo originale

Solstizio d'estate

Per inaugurare il rientro dalla settimana vacanziera auspico un buon solstizio d'estate a tutti. (Anche se con i 12,5° di stamane non si direbbe proprio.)
Per chi volesse brindare con un po' più di precisione dovrà farlo alle 11:28.

Carnevale della Matematica #26: Russell e la logica (quasi una monografia)

"Uomo di sani Principia, tra una moglie e l'altra spedi paradossalmente una tazza di tè nello spazio."

E' questa la biografia essenziale di Bertrand Russell, che Gianluigi Filippelli propone per introdurre il tema non obbligatorio proposto per il Carnevale numero 26: Russell e la logica.
"La motivazione del tema è dovuta al recente compleanno dello zio Bertrand, nato il 18 maggio 1872, quindi in una data compresa tra questo e il Carnevale precedente, ospitato dalla grandissima Annarita Ruberto".

Il mio contributo viene introdotto Gianluigi (che ringrazio per la bella recensione) in questo modo:

Dioniso, per l'occasione del tema, interrompendo il suo classico percorso storico tra i numeri e ci propone una bellissima tetralogia logica scritta attraverso una serie di dialoghi immaginari dal titolo Il mondo finirà nel 2012? Una questione di Logica modale temporale?: nella prima parte protagonisti sono Aristotele e Diodoro Crono; nella seconda parte vengono presentate alcune Rubʿayyāt di ʿOmar Ḫayyām⁽¹⁾, ovvero delle quartine dove vengono descritti i sogni/incubi di Avicenna, logico e matematico persiano, nei quali il nostro dialoga fittamente con Aristotele; nella terza parte protagonisti sono Leibiniz e Voltaire in un testo attribuito a Pierre Beaumarchais dove si esamina l'affermazione Maya sulla fine del mondo alla luce delle novità logiche di quel periodo, fine 1600 inizi 1700, quando la logica occidentale inizia veramente a muovere i primi passi; nella quarta e ultima parte dove, prendendo spunto dalle rivoluzioni introdotte da Frege e Russell⁽²⁾ (e dalla sua scuola) esamina con i metodi e le notazioni della logica della prima metà del XX secolo l'affermazione incriminata (e quelle che poi i soliti folli giornalisti non smettono di disseminare in giro per il mondo).
Nel complesso una tetralogia veramente molto bella, quasi quanto le famose tetralogie di Leonardo Ortolani su RatMan Collection, che ha il pregio, nonostante i dialoghi siano nei fatti frutto dell'immaginazione di Flavio, di sintetizzare al meglio il pensiero logico dei protagonisti. Da non perdere!

Calendario con le date delle prossime edizioni del Carnevale

Pagina fan del Carnevale su Facebook

Riportando tutto a casa - Nicola Lagioia

Imperdibile!

...soprattutto per chi come me ha vissuto la propria adolescenza negli anni '80...

Recensioni: Jacopo Tondelli, Daniele Greco
Intervista a Nicola Lagioia
Nicola Lagioia

Il mondo finirà nel 2012? Una questione di Logica modale? - quarta parte

Nella puntata precedente abbiamo visto che l'idea leibniziana dei mondi possibili ci è stata utile per la comprensione della questione Maya. Ci chiedevamo inoltre che cosa significa che le assiomatizzazioni della Logica modale vennero inquadrate in ambito più logico matematico?

La Logica matematica come disciplina indipendente dalla Logica tradizionale nasce nella seconda metà del XIX secolo. Si parte in qualche modo ancora una volta dalla Logica aristotelica ponendosi però in una prospettiva molto più formale e inquadrando il linguaggio delle Logica in un contesto molto vicino a quello dell'algebra astratta. Questa nuova disciplina parve presto molto adatta per indagare quelle questioni dei fondamenti della Matematica che da qualche tempo turbavano i sonni di alcuni grandi matematici. Tanto che Gottlob Frege elaborò il progetto di poter costruire tutta la matematica a partire dalla logica, riducendo così la seconda alla prima.

Purtroppo però, dopo anni di studi e pubblicazioni, gli ambiziosi progetti di Frege si infransero contro una lettera di Bertrand Russell in cui il logico matematico inglese demoliva tutto il lavoro di Frege con un solo semplice paradosso mostrando così, con grande dispiacere di tutti, anche di Russel stesso, che la matematica non è riducibile alla logica. Si ripartì con il tentativo di Peano di ridurre tutta la matematica all'aritmetica, e quello di Russell che nei Principia Mathematica risolse i problemi contro i quali si era infranto il sogno di Frege.
La parola definitiva spettò tuttavia al giovanissimo Kurt Gödel, che nel 1931, a soli venticinque anni, pubblicò i suoi celeberrimi teoremi di incompletezza che provavano come nessun sistema logico finitamente assiomatizzabile potesse risolvere dentro di sé tutte le verità della matematica. O detto in altre semplificanti parole, non si possono catturare tutte le verità della matematica a partire da un numero finito di assiomi. Dunque l'idea di Euclide secondo cui a partire da pochi assiomi si possono derivare tutte le verità di un certo sistema risultò non applicabile all'intera matematica. Mentre in seguito si dimostrò (Tarski) che quell'idea continuava ad essere valida per sistemi più deboli, come appunto la Geometria euclidea, ma anche la Logica proposizionale. Invece nel momento in cui si aggiunge l'Aritmetica, così come la intendiamo comunemente, intervengono i teoremi di Gödel a rendere inapplicabile l'idea euclidea.

Ma questo discorso esula un po' dal nostro scopo e meriterebbe sicuramente uno o più capitoli di approfondimento che molto probabilmente saranno presenti tra gli articoli del Carnevale della Matematica numero 26 del 14 giugno 2010.

Per tornare al nostro discorso sulla Logica modale inquadrata nell'ambito logico matematico possiamo partire dalla considerazione che la Logica modale è un'estensione della Logica proposizionale. Qui qualcuno potrebbe chiedersi: e che cos'è la Logica proposizionale?

La Logica proposizionale come la maggior parte dei sistemi di Logica matematica è costituita da una parte sintattica ed una parte semantica.
La parte sintattica è quella che si occupa di definire la corretta struttura delle proposizioni; e nella quale si include di solito anche l'apparato deduttivo che definisce gli assiomi e le regole che consentono di dedurre i teoremi a partire dagli assiomi.
Mentre la parte semantica, che risulta di solito più semplice ed intuitiva, è quella che si occupa di definire il significato dei simboli.
Pertanto, volendo partire da un esempio con la nostra proposizione Maya, indicheremo con:

M la proposizione Maya: "Il 21 dicembre 2012 finirà il mondo"
B la proposizione del buco nero: "Il 21 dicembre 2012 l'LHC del CERN produrrà un buco nero"
G la proposizione della guerra nucleare: "Il 20 dicembre 2012 scoppierà una guerra nucleare"

Nella Logica matematica si usa il simbolo "¬" per indicare la negazione di una proposizione. Nel nostro caso pertanto ¬M rappresenterà la proposizione non Maya. I simboli "→" e "∧" rappresentano invece rispettivamente l'implicazione la congiunzione. Ad esempio nel nostro caso:

B → M si tradurrebbe con: se "Il 21 dicembre 2012 l'LHC del CERN produrrà un buco nero" allora "Il 21 dicembre 2012 finirà il mondo"
G → M si tradurrebbe con: se "Il 20 dicembre 2012 scoppierà una guerra nucleare" allora "il 21 dicembre 2012 finirà il mondo"
B ∧ G → M si tradurrebbe con: se "Il 21 dicembre 2012 l'LHC del CERN produrrà un buco nero" e "Il 20 dicembre 2012 scoppierà una guerra nucleare" allora "Il 21 dicembre 2012 finirà il mondo"

A questo punto possediamo tre proposizioni composte secondo le regole della sintassi proposizionale:
B → M, G → M e B ∧ G → M. E potremmo trattarle come pure sequenze di simboli prive di significato e manipolarle attraverso le regole di una qualche apparato deduttivo rimanendo così nell'ambito sintattico.
Oppure, come abbiamo fatto qui sopra, potremmo attribuire un significato alle formule e cercare di assegnar loro un valore di verità: cioè capire se esse sono vere o false. E in questo caso ci troveremmo nel dominio della semantica della Logica proposizionale.
Ma come facciamo ad asserire che B → M è vera? Siamo sicuri che l'eventuale buco nero prodotto al CERN inghiottirebbe la Terra? Una domanda simile potremmo porcela per la guerra nucleare (G → M) e per la concomitanza dei due eventi (B ∧ G → M): siamo sicuri che sterminerebbero il genere umano?.

Potremmo considerare ad esempio che a seconda della microscopicità e della instabilità del buco nero o a seconda della violenza e dell'estensione della guerra potrebbero verificarsi esiti diversi. È qui che entra in gioco la Logica modale con la sua semantica, che Saul Kripke definì nel 1959 a soli 19 anni basandosi sul concetto Leibniziano dei mondi possibili.
La semantica di Kripke definisce matematicamente il concetto di mondo possibile e poi definisce una proposizione M come necessariamente vera, in simboli □M, quando essa è vera in tutti i mondi possibili e come possibilmente vera, in simboli ◊M, quando essa è vera in almeno un mondo possibile.
Usando quindi la sintassi e la semantica modali potremmo tornare ad interrogarci sulla verità di

B → M: se "Il 21 dicembre 2012 l'LHC del CERN produrrà un buco nero" allora "Il 21 dicembre 2012 finirà il mondo"

B → M è necessariamente vera?
□(B → M)

Oppure è possibilmente vera?
◊(B → M)

Personalmente propenderei più per la seconda ipotesi, viste le precedenti considerazioni sulla microscopicità e sulla instabilità del buco nero.
In realtà se andiamo poi a leggere la pagina del CERN che parla della sicurezza dell'LHC dovremmo forse concludere che l'evento è impossibile e cioè:
¬◊(B → M)

Che equivale ad affermare la necessita della sua negazione e cioè:
□¬(B → M)

Ho l'impressione che tutto questo discorso potrebbe anche essere stato affrontato sotto una prospettiva probabilistico-bayesiana, ma questo magari lo rimandiamo ad un futuro anniversario di Bayes.

Concludo con:

1. le formule fondamentali per la Logica modale classica:

2. un brevissimo cenno al fatto che esiste anche una Logica modale intuizionista (non classica) che è un'estensione della Logica proposizionale intuizionista, in cui le suddette formule fondamentali non valgono e che alcuni anni fa mi causò diverse notti insonni.

3. la clausola di esonero della responsabilità a scanso di equivoci:

I dialoghi di questi quattro post sono frutto dell'immaginazione dell'autore e sono stati usati solo come espediente narrativo.

C'è una teiera di porcellana che orbita attorno al Sole

La teiera di Russel (Post ispirato da Arimortis)

«Se io sostenessi che tra la Terra e Marte c'è una teiera di porcellana in rivoluzione attorno al Sole su un'orbita ellittica, nessuno potrebbe contraddire la mia ipotesi, purché mi assicuri di aggiungere che la teiera è troppo piccola per essere rivelata, sia pure dal più potente dei nostri telescopi. Ma se io dicessi che - posto che la mia asserzione non può essere confutata - dubitarne sarebbe un'intollerabile presunzione da parte della ragione umana, si penserebbe con tutta ragione che sto dicendo fesserie. Se, invece, l'esistenza di una tale teiera venisse affermata in libri antichi, insegnata ogni domenica come la sacra verità ed instillata nelle menti dei bambini a scuola, l'esitazione nel credere alla sua esistenza diverrebbe un segno di eccentricità e porterebbe il dubbioso all'attenzione dello psichiatra in un'età illuminata o dell'Inquisitore in un tempo antecedente.»

Bertrand Russel

Il mondo finirà nel 2012? Una questione di Logica modale? - terza parte

Abbiamo visto che il sillogismo avicenniano non è risultato utile a sciogliere il groviglio della questione Maya-Saclà, riassunta nella proposizione:

Il 21 dicembre 2012 finirà il mondo

Vediamo allora se spostandoci avanti nella storia riusciremo a trovare nuovi strumenti modali utili a dirimere la nostra diatriba.

La Logica avicenniana esercitò una certa influenza in Europa occidentale sugli scolastici che svilupparono una particolare attenzione alle modalità, e soprattutto ai concetti di possibilità e necessità. È proprio alla tradizione scolastica infatti che si deve la definizione di "modale" per questo tipo di Logica. Modale in quanto indica il modo in cui una proposizione è vera: necessariamente o possibilmente.
Tuttavia neppure gli scolastici svilupparono strumenti logici adatti al nostro scopo.

Quello che invece potrebbe aiutarci è un altro documento, che mi è capitato tra le mani a Parigi in una libreria dell'usato nel quartiere di Marais. Stavolta la lingua è il francese. La traduzione non presenta quindi difficoltà estreme.
Con mio sommo stupore mi rendo conto di trovarmi per la terza volta di fronte ad un inedito. L'autore è Pierre Beaumarchais e il testo è di nuovo un dialogo avvenuto stavolta nel secondo decennio del XVIII secolo tra il vecchio Leibniz e il ventenne Voltaire. Pare che quel dialogo sia stato narrato a Beaumarchais dalla cameriera di Voltaire che intratteneva rapporti di stretta amicizia con il giovane autore de "Il barbiere di Siviglia". Alcune dicerie del tempo riportano che uno dei criteri con cui Voltaire sceglieva le cameriere era basato sulla competenza storico-filosofica delle giovani aspiranti. Ma leggiamo il dialogo.

L: (con stanca e annoiata prosopopea) Vedete giovane Arouet (ndD lo pseudonimo di "Voltaire" fu assunto dal filosofo solo nel 1718), in questo nostro mondo, che è indubbiamente il migliore tra tutti i possibili mondi, tutti i fatti sono interconnessi tra loro. Tanto è vero che, se voi non foste stato scacciato a gran calci nel sedere da uno dei più bei castelli di Provenza ed allontanato a malo modo dalla bella Cunegonda, ora non sareste qui a beneficiare di questo dialogo con il più grande matematico e filosofo vivente. Pertanto, ciò che all'inizio poteva apparire come un inconveniente si è rivelato essere un grosso vantaggio per il vostro sviluppo intellettuale.

V: (con evidente insoddisfazione) Voi dite bene, esimio Leibniz, ma non potremmo forse immaginare un altro mondo possibile in cui io non sia stato scacciato a gran calci nel sedere ed ora mi trovi nel castello provenzale della mia bella Cunegonda a dialogare con il più grande matematico e fisico vivente, Sir Isaac Newton?



L: (apodittico) Il nostro mondo deve essere necessariamente il migliore e il più equilibrato tra i mondi possibili, in quanto creato da un Dio perfetto. Il Suo imperscrutabile disegno può apparire imperfetto alle nostre miserevoli menti umane, ma la vostra scacciata, in quanto parte del disegno di un Essere perfetto, non può che essere stata concepita per il meglio possibile.

V: (meditabondo) Ma allora, se tutto è stato concepito per il meglio possibile, la proposizione Maya:

"Il 21 dicembre 2012 finirà il mondo"

dovrebbe essere impossibile? Visto che se fosse vera non sarebbe stata concepita per il meglio possibile .... A meno che il meglio possibile per l'Universo non sia rappresentato proprio dalla scomparsa del genere umano o dell'Universo stesso ....
O forse no! La proposizione Maya potrebbe essere possibile ma comunque falsa nel nostro mondo. Infatti potremmo senz'altro immaginare un altro mondo possibile, ben lungi dall'essere il migliore, in cui la proposizione Maya sia vera... E certo! Potremmo immaginare un mondo possibile in cui il 21 dicembre 2012 si verifichi un evento catastrofico planetario o addirittura universale.
Pertanto la proposizione Maya non è impossibile! Difatti, per poterla dichiarare impossibile dovremmo poter asserire la sua falsità in tutti i mondi possibili. In tal caso sarebbe necessaria la sua negazione. Cioè la proposizione non Maya:

"Il 21 dicembre 2012 non finirà il mondo"

Necessaria in quanto vera in tutti i mondi possibili. Ma abbiamo appena visto che si possono concepire dei mondi in cui la proposizione Maya è vera.
Penso che questo potrebbe essere un buon argomento di discussione per il giorno del mio ritorno al castello della bella Cunegonda. E sono abbastanza sicuro che questa mia conclusione sarebbe piaciuta ad Aristotele.

La  storia purtroppo ignora anche questo dialogo, ma ci dice tuttavia che la paternità dell'idea dei mondi possibili è effettivamente attribuita a Leibniz.
La storia ci dice inoltre che la Logica modale moderna nascerà circa due secoli dopo Leibniz con le assiomatizzazioni pubblicate nel 1932 da C. I . Lewis nel libro Symbolic Logic. Due decenni dopo queste assiomatizzazioni vennero inquadrate in ambito più logico matematico soprattutto ad opera di Alfred Tarski.
Ma che cosa significa "in ambito più logico matematico"? E soprattutto, questo ambito ci aiuterà nella comprensione della questione Maya? Lo vedremo nella quarta ed ultima parte.

Il suddito ideale

Il suddito ideale del regime totalitario non è il nazista convinto o il comunista convinto, ma l’individuo per il quale la distinzione fra realtà e finzione, fra vero e falso non esiste più»

(Hannah Arendt Le origini del totalitarismo, 1951)

Il mondo finirà nel 2012? Una questione di Logica modale temporale? - seconda parte

Abbiamo visto che alcune considerazioni sulla Logica modale sono comparse per la prima volta nella storia nel IV secolo a.C. ad opera di Aristotele e Diodoro Crono. E che queste considerazioni si sono rivelate utili per aiutarci a districare la questione Maya e la sua proposizione:

Il 21 dicembre 2012 finirà il mondo

Nella prima parte l'arguto Fabio di Einbahnstrasse mi faceva notare che il mondo non potrà finire nel 2012 visto che il suo barattolo di sottaceti riporta il 2013 come anno di scadenza.
Ma allora la proposizione Maya è necessariamente falsa!?
I Maya si erano sbagliati e sono stati clamorosamente smentiti dalla Saclà?
La competizione si fa interessante: una multinazionale gastronomica contro una delle civiltà più affascinanti della storia umana....
Chi uscirà vincitore i Maya o la Saclà?

Vediamo se riusciremo a trovare nella Logica modale qualche altro appiglio che ci possa aiutare a dipanare questo scontro tra titani....

Dopo Aristotele e Diodoro Crono dovrà trascorrere più di un millennio prima che si possano trovare ulteriori progressi nell'ambito della Logica modale. A svilupparli fu il medico, filosofo, matematico e fisico persiano Ibn Sina più noto in occidente come Avicenna (Balkh, 980 – Hamadan, 1037).

Per questa seconda parte mi avvarrò di un altro documento acquistato anch'esso durante uno dei nostri viaggi. Questa volta però un po' più a oriente. In Giordania. E per la precisione nel sūq di Amman. Dove, oltre che dal libro di ricette che ha fatto entrare l'hummos nel nostro ricettario familiare, fui anche stranamente attratto da un vecchio libricino scritto in arabo. Lingua totalmente ignota sia a me che a Zucchero. Dovemmo attendere infatti diversi anni prima di poter leggere una traduzione di quel libricino. Ce lo tradusse il nostro ex-collega Khaled. Con grande sorpresa scoprii che si trattava di alcune Rubʿayyāt di ʿOmar Ḫayyām che si credevano smarrite. Tali quartine narrano, in forma di brevi dialoghi, gli incubi che tormentarono Avicenna per un periodo di mille e una notte. Incubi in cui lo scienziato persiano veniva visitato dal filosofo greco Aristotele, il quale cercava di persuadere Avicenna dell'univocità interpretativa della realtà attraverso la Logica aristotelica. In anteprima mondiale riporto di seguito la traduzione delle ultime quartine del poema che riportano il dialogo avvenuto durante la milleunesima notte. Il mio ex-collega mi informa che purtroppo, per questioni di praticità, la bella metrica poetica delle quartine arabe si è persa con la traduzione.

Ar: (con insolenza) Caro Avicenna, devo confessarVi che tra le mie creazioni intelettuali che Vi ho illustrato nelle mille notti precedenti quella di cui vado più fiero, e che rimarrà un monumento imperituro alla ragione umana, è il mio sillogismo:
• (premessa maggiore) Tutti gli uomini sono mortali
• (premessa minore) Socrate è un uomo
• (conclusione) Socrate è mortale


Av: (riflessivo) Illustre Aristotele, vorrei sottoporVi il seguente esempio di applicazione del Vostro sillogismo:
• (premessa maggiore) Tutti gli uccelli volano
• (premessa minore) Tutti i pinguini sono uccelli
• (conclusione) Tutti i pinguini volano

Ar: (con titubanza) Ehm, ... la Vostra premessa maggiore... forse... andrebbe interpretata...

Av: (con crescente entusiasmo) È con sommo dispiacere che mi trovo in questa imbarazzante condizione di doverVi far notare una lacuna nel Vostro "monumento imperituro alla ragione umana".
(con decisione) Questa lacuna potrebbe però essere colmata con l'inserimento di operatori quali "sempre" e "quasi sempre"
• (premessa maggiore) Tutti gli uccelli volano (quasi sempre)
• (premessa minore) Tutti i pinguini sono uccelli (sempre)
• (conclusione) ?

La figura onirica di Aristotele impallidisce, si fa sempre più diafana, fino a scomparire del tutto.

Av:(con sollievo) Finalmente potrò trascorrere notti tranquille....

Tuttavia la storia ufficiale ignora questo dialogo e ci dice che Avicenna fu il primo a fornire un vero e proprio sistema formale per la Logica modale temporale costruendo così quella che in seguito venne chiamata la Logica avicenniana; che nasce proprio dalla critica di Avicenna alla Logica aristotelica. Critica che condusse lo scienziato persiano a sviluppare un forma modale temporale del sillogismo introducendo nelle premesse operatori temporali quali "sempre", "quasi sempre", e "a volte". Nel dialogo che abbiamo visto gli operatori non sono propriamente temporali. Il risultato semantico è diverso ma quello sintattico non cambia.

Ma tornando ai Maya, il sillogismo avicenniano ci fornisce qualche strumento aggiuntivo che possa essere utile a sbrogliare lo gnommero gaddiano della questione?
Non parrebbe. La questione Maya è espressa da una semplice proposizione e non da un sillogismo! A meno che qualcuno non si voglia spingere ad accettare come premessa maggiore che i Maya sono infallibili....
In caso contrario dovremo spostarci di nuovo avanti nella storia alla ricerca di nuovi strumenti modali.
Ma questo lo vedremo nella terza parte.

Vivi dell'oggi e non perdere al vento la vita

Non ricordare il giorno trascorso
e non perderti in lacrime sul domani che viene:
su passato e futuro non far fondamento
vivi dell'oggi e non perdere al vento la vita.
(ʿOmar Ḫayyām, Rubʿayyāt)
از دی که گذشت هیچ از او یاد مکن
فردا که نیامده‌ست فریاد مکن
بر نامده و گذشته بنیاد مکن
حالی خوش باش و عمر بر باد مکن